Merge Algorithm (Kotlin Code)
The Problem Statement:
You are given two sorted arrays.
you need to merge them into a sorted array.
Example :
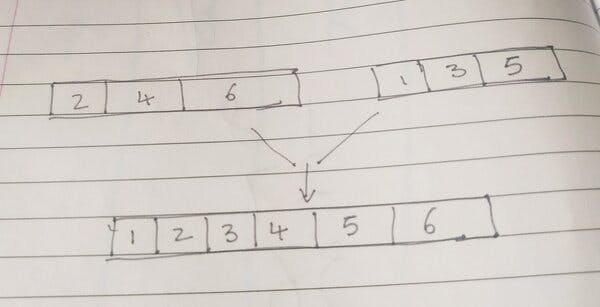
The Elevator Pitch of the solution:
First compare the first element of each input array.
(2,1)
Pick the smaller element and add it to the output array.
(add 1 to output)
Now we need to add the next element to output array, so :
Increase pointer of output array.
(output pointer becomes 1 from previous value of 0)
Increase pointer of the array that we used to pick the first element.
(odd number arrays pointer now points to second element)
Keep doing above steps until all elements of one input array are completely added to the output array.
copy all remaining elements of the other input array to the output array.
Dry Runs:


Algorithm:
Merge(A,B){
m = A.size, n = B.size
C = Array(m+n)
i = j = k = 0
while(i < m && j < n)
{
if(A[i] < B[j])
C[k++] = A[i++]
else
C[k++] = B[j++]
}
//copy remaining below
while(i < m)
C[k++] = A[i++]
while(j < n)
C[k++] = B[j++]
}
fun twoWayMerge(a:IntArray,b:IntArray):IntArray{
val m = a.size; val n = b.size
val c = IntArray(m+n)
var i = 0; var j = 0; var k = 0
while(i < m && j < n){
if(a[i] < b[j]){
c[k++] = a[i++]
}
else{
c[k++] = b[j++]
}
}
while(i < m){
c[k++] = a[i++]
}
while(j < m){
c[k++] = b[j++]
}
return c
}
fun main() {
twoWayMerge(intArrayOf(2,4,6),intArrayOf(1,3,5)).let{
it.forEach {
println(it)
}
}
}
